Perfect Numbers and How to Find Them

Perfect numbers have long been studied in ancient history, the first were probably studied many millennia ago. A perfect number is, by definition, a positive integer where the sum of its factors except itself is equal to it.
Throughout history perfect numbers have been thought to have mystic powers. For example, the Pythagoreans studied them for that very purpose. Many have regarded perfect numbers as biblical and referring to the divine, for example the 28-day cycle of the moon is seen as heavenly and God is said to have created the world in 6 days (28 and 6 both being perfect numbers). This is why many Christian thinkers have looked particularly at perfect numbers and biblical events, a famous quote from St Augustine writing in the city of God is, “ Six is a number perfect in itself, and not because God created all things in six days; rather, the converse is true. God created all things in six days because the number is perfect. “. Showing that some of the greatest Christian thinkers take great credence in the theory that perfect numbers have more than just mathematical relevance. The first known and existing mathematical theory on perfect numbers, comes in Euclid’s Elements. He proves the hypothesis that by doubling from 1 and adding all the numbers together until you reach a prime number, and multiplying that prime by the last double, equals a perfect number. For example, 1+2+4=7, 7*4=28 and 28 is a perfect number. However, Euclid did not stop there, he also theorised 2k−1(2k−1) is always a perfect number providing that 2k-1 is prime and k is greater than 1. Although he knew a perfect number would always be created in these conditions, he did not know that every even perfect number would follow this formula. It took Leonhard Euler in the 18th century to discover this. It is not yet known whether there are any odd perfect numbers.
At the beginning of this project, I was set a challenge, to write a code which could find all the perfect numbers in a certain range. This piece of code was my first step towards this.


This was my earliest, most primitive piece of code. The user inputs an integer. And an iteration statement repeats the next piece of code the number minus one times, for example, if six was the number the code would be repeated 5 times. Then the % function is used to find the remainder of the number input divided by the loop (which starts counting from 0 and measures which repeat we are on) + 2. After this, integer division (//) is used to find the answer to the number divided by the loop + 2 without remainder (giving an integer answer). Finally, a selection (if) statement is used to check if there is a remainder or not when the number inputted is divided by the loop + 2. If there is no remainder, then the answer to the number divided by the loop + 2 is appended to the list “factors”. Basically, what this part of the code is checking if the number inputted divided by any given number from 2 upwards until the number itself has an integer answer, and if the answer is an integer, it is added to the list ‘factors’. The next line after the for loop, is used to assign the value of all the numbers in the list ‘factors’ added together, to the variable ‘z’. After this line, is a selection statement which means that if the sum of the list factors is 0 it becomes 1. This means that if the number inputted is 0, the code does not print, ‘This is a perfect number’. Important, as 0 is not a perfect number. Finally, the last selection statement checks if z (the sum of the list factors) is equal to the number which is greater than 1, and if it is, prints “This is a perfect number. Otherwise, if the sum of the factors does not equal the number. “This is not a perfect number” is printed. Basically, this code checks if any number inputted is a perfect number.
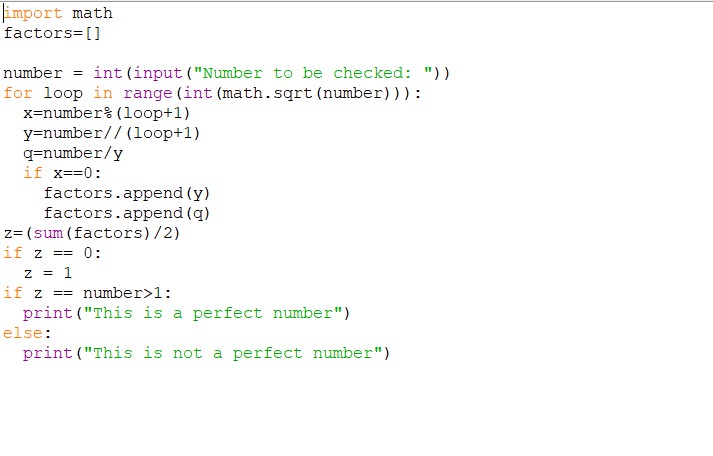 However, there was an issue, with this code. The sheer number of calculations the computer had to make, meant that when the perfect numbers got into the billions, the computer took much longer to test if the number was a perfect number. This inspired my next piece of code.
However, there was an issue, with this code. The sheer number of calculations the computer had to make, meant that when the perfect numbers got into the billions, the computer took much longer to test if the number was a perfect number. This inspired my next piece of code.
This piece of code is very similar to the previous piece; however, it is optimised to decrease the amount of calculations that need to be done, therefore decreasing the time needed to check larger numbers. As you can see, the code starts slightly differently to the previous piece. This time, I have imported math. This allows me to square root a number, crucial in this program. The difference with this code is that the for loop is repeated a number of times equal to the square root of the number rounded down to the nearest integer, instead of the number – 1. This difference means the number of calculations goes down exponentially, and all the factors can still be found. The next three lines in order; find the remainder of the number divided by the loop + 1; integer divide the number by the loop + 1; and divide the number by the integer division of the number by the loop + 1. If we go through an example of this with the number six. Six will first be divided by 1 and the remainder will be the value of x. Then six is divided by 1 again, and the answer to this will be the value of y. Finally, the number is divided by y and in this case, we will be given the answer 1 which will be the value of q. Finally, if the value of x was 0, both y and q will be added to the list factors. This process will be repeated for all the numbers up to the rounded down square root of the initial number. Then the numbers in factors are all added up and divided by 2. They are divided by 2 because the initial number will also be in the factors list. Then the process is the same as the previous piece of code.
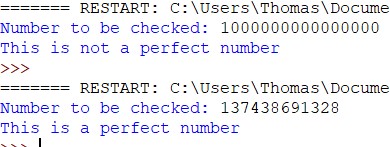 This was a considerable improvement on the last program. Where the previous program was only able to quickly calculate up to 8 or 9 digits, this program can calculate up to 15 digits quickly. Although this was not the completion of my challenge, this was definitely a step in the right direction.
This was a considerable improvement on the last program. Where the previous program was only able to quickly calculate up to 8 or 9 digits, this program can calculate up to 15 digits quickly. Although this was not the completion of my challenge, this was definitely a step in the right direction. This was the final evolution of my code, a program which could find all the even perfect number up to a point. This program uses the link between Mersenne primes and perfect numbers to do this. This code also uses the foundations of the previous programs to achieve the goal. The code starts with; the creation of two lists, perfects, and factors; the importing of math; and the creation of the variable k, which has the value 0. Next there is an iteration statement which repeats 25 times. This is what you change in the code to affect the range of numbers which it will test. Inside the for loop is first a piece of code that means in every iteration, k is increased by 1, and following that, is the most important line of code. This line allows us to calculate the possible perfect numbers. It works on the fact that if you multiply a prime number that can be expressed by (2k−1) by 2k−1 you get a perfect number. As there is no simple code I know of to test for primes on python, instead of only using primes that can be expressed by (2k−1), I used every positive integer which could be expressed by the formula in a certain range where k is an integer, so I ended up calculating every possibility of k up to the number of times my code repeats. Therefore, I had to check each number I had previously calculated to see if it was a perfect number. To do this, I used the code from before, which could tell if any number is a perfect number. After this code, came
This was the final evolution of my code, a program which could find all the even perfect number up to a point. This program uses the link between Mersenne primes and perfect numbers to do this. This code also uses the foundations of the previous programs to achieve the goal. The code starts with; the creation of two lists, perfects, and factors; the importing of math; and the creation of the variable k, which has the value 0. Next there is an iteration statement which repeats 25 times. This is what you change in the code to affect the range of numbers which it will test. Inside the for loop is first a piece of code that means in every iteration, k is increased by 1, and following that, is the most important line of code. This line allows us to calculate the possible perfect numbers. It works on the fact that if you multiply a prime number that can be expressed by (2k−1) by 2k−1 you get a perfect number. As there is no simple code I know of to test for primes on python, instead of only using primes that can be expressed by (2k−1), I used every positive integer which could be expressed by the formula in a certain range where k is an integer, so I ended up calculating every possibility of k up to the number of times my code repeats. Therefore, I had to check each number I had previously calculated to see if it was a perfect number. To do this, I used the code from before, which could tell if any number is a perfect number. After this code, came 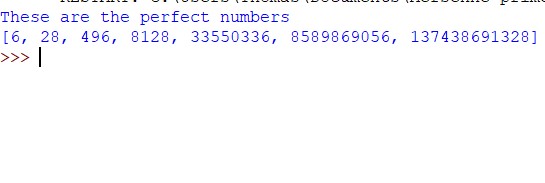 another vital line, the factors.clear() line. This allowed me to clear the list, ‘factors’ after each number was checked, meaning that it would not keep the factors of all the previous numbers, therefore meaning I could check the factors of multiple numbers. Then, if the number was perfect, I added it to the list perfects, and then printed that list.
another vital line, the factors.clear() line. This allowed me to clear the list, ‘factors’ after each number was checked, meaning that it would not keep the factors of all the previous numbers, therefore meaning I could check the factors of multiple numbers. Then, if the number was perfect, I added it to the list perfects, and then printed that list.
However, I did not complete the challenge fully, as my code relied on a range of values of ‘k’ in the formula 2k−1(2k−1). Rather than calculating all the perfect numbers in a range, e.g. 1-1000. However, if I did do a range of numbers, and it was say, 1-10 billion was the range. It would take quite a long time to calculate, so my code is more efficient than a program which calculates all the perfect numbers in a range. Also, another issue with my last program, is that it does not consider the possibility of odd perfect numbers, and only tries to find even ones. Which is the limitation of using the formula 2k−1(2k−1), as, discounting 1, the formula only produces even numbers. Something which using a range of numbers would solve, but as I mentioned previously, there are many drawbacks to a range system.
Theoretically, if you keep increasing the number of times the code repeats, (the number in the “for loop in range” line) and you were willing to wait long enough for the computer to calculate if all those numbers were perfect numbers, you could find new even perfect numbers. However, lacking a supercomputer, you would be waiting for quite a while.
Bibliography
Britannica-https://www.britannica.com/science/perfect-number
https://mathshistory.st-andrews.ac.uk/HistTopics/Perfect_numbers/














